Introduction:

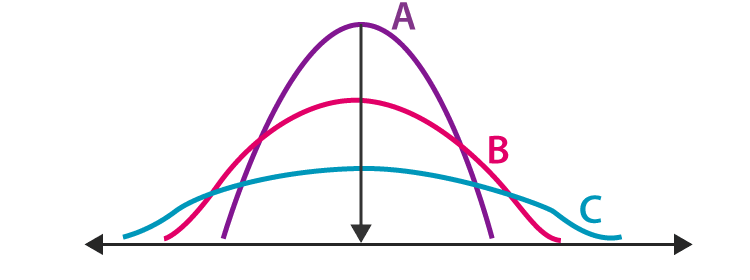
Measures of dispersion are used to describe the spread or variability of a dataset. The interquartile range (IQR) is a commonly used measure of dispersion that provides information about the middle 50% of the data. In this article, we will explore the advantages of using IQR compared to other measures of dispersion.

What is IQR?

IQR is the range of the middle 50% of the data in a dataset. It is calculated as the difference between the third quartile (Q3) and the first quartile (Q1). In other words, IQR represents the spread of the data that excludes the top and bottom 25% of the values, calculated by using IQR calculator

Other measures of dispersion:

Other measures of dispersion include the range, variance, and standard deviation. The range is the difference between the largest and smallest values in the dataset. The variance is the average of the squared differences from the mean, while the standard deviation is the square root of the variance.

While each of these measures has its own advantages and disadvantages, IQR offers several unique benefits that make it a useful measure of dispersion in many situations.

Advantages of using IQR:

a. Robustness to outliers:

One of the primary advantages of using IQR compared to other measures of dispersion is its robustness to outliers. Outliers are extreme values that are much larger or smaller than the other values in the dataset. These outliers can have a significant impact on measures of dispersion like the range, variance, and standard deviation, which are all sensitive to extreme values. IQR, on the other hand, is less affected by outliers because it only considers the middle 50% of the data. This makes IQR a more reliable measure of dispersion in datasets that contain outliers.

b. Ease of interpretation:

Another advantage of IQR is its ease of interpretation. Unlike the variance and standard deviation, which are expressed in squared units, IQR is expressed in the same units as the original data. This makes it easier to understand and communicate the spread of the data to others who may not be familiar with statistical terminology.

c. Less affected by extreme values:

IQR is also less affected by extreme values compared to other measures of dispersion. In datasets with extreme values, the range, variance, and standard deviation can be very large, making it difficult to interpret the spread of the data. IQR, on the other hand, only considers the middle 50% of the data, so extreme values have less of an impact on its calculation.

In summary, IQR offers several advantages over other measures of dispersion, including its robustness to outliers, ease of interpretation, and resistance to extreme values. These benefits make IQR a useful tool for describing the spread of data in a variety of settings.

Disadvantages of using IQR:

While IQR has several advantages, there are also some limitations to its use. One potential disadvantage of IQR is that it only provides information about the middle 50% of the data. This means that it may not be a suitable measure of dispersion for datasets where the extreme values are important.

Another limitation of IQR is that it does not provide information about the shape of the distribution of the data. Measures of central tendency, such as the mean and median, are better suited for describing the shape of the distribution.

Conclusion:

In conclusion, IQR is a useful measure of dispersion that has several advantages over other measures, including its robustness to outliers, ease of interpretation, and resistance to extreme values. However, it is important to consider the limitations of IQR, such as its inability to describe the shape of the distribution and its focus on only the middle 50% of the data. Overall, IQR can be a valuable tool for describing the spread of data in many situations, but it should be used in conjunction with other measures of dispersion and descriptive statistics to provide a comprehensive understanding of the data.

References:

Pizzi, N. J., & Ritter, G. W. (1992). Using the interquartile range to determine outliers. Journal of Nursing Measurement, 1(3), 205-217.

Tukey, J. W. (1977). Exploratory data analysis. Addison-Wesley.

Appendices

FAQ’s

What makes IQR more robust to outliers than other measures of dispersion?

IQR is more robust to outliers than other measures of dispersion because it only considers the middle 50% of the data, which is less affected by extreme values. Other measures of dispersion, such as the range, variance, and standard deviation, are more sensitive to extreme values and can be heavily influenced by outliers.

Can IQR be used as the sole measure of dispersion in all datasets?

While IQR is a useful measure of dispersion, it may not be suitable for all datasets. In some cases, extreme values may be important and need to be taken into account when describing the spread of the data. Additionally, IQR does not provide information about the shape of the distribution, so it should be used in conjunction with other descriptive statistics to provide a comprehensive understanding of the data.

How does the ease of interpretation of IQR compare to other measures of dispersion?

One of the advantages of IQR is its ease of interpretation compared to other measures of dispersion. While the variance and standard deviation are expressed in squared units, which can be more difficult to understand, IQR is expressed in the same units as the original data. This makes it easier to communicate the spread of the data to others who may not be familiar with statistical terminology.

Additional Resources 

https://iqrcalculator.com